Všetky cesty vedú do Ríma (k Normálnemu rozdeleniu)

 

V súčasnosti, dávam Normálnemu rozdeleniu veľký priestor v článkoch, no ako sami vidíte – je to potrebné. Existujú isté cesty, alebo povedzme dôkazy pomocou ktorých si môžeme zjednodušiť štatistický život tak, že budeme používať user friendly - Normálne rozdelenie. My si totižto empiricky ukážeme, že Binomicky, Poissonovo rozdelenú a všeobecne akúkoľvek náhodnú veličinu môžeme pri dostatočnom množstve dát bezpečne popísať Normálnym rozdelením vďaka ich aproximácii.

Jedná sa o tzv. limitné vety. No na začiatok si ukážeme, že Binomické rozdelenie pri veľkom počte možných náhodných javov a nízkej pravdepodobnosti aproximuje k Poissonovmu rozdeleniu.

V priloženom sample file-e si môžete prezrieť výpočty, no ako ilustrácia poslúži obrázok grafov rozdelení pre rôzne parametre binomického rozdelenia:




Moivreova-Laplaceova veta

Uvažujme proces, ktorým by sme mohli generovať možné výsledky náhodnej veličiny. Povedzme Alternatívnym rozdelením by sme generovali hodnoty x₁ ; x₂ … atď. Každá hodnota je generovaná nezávisle na výsledku predchádzajúcich hodnôt (Dôležitý predpoklad!).

Čo s takto danými hodnotami náhodných veličín? Môžeme uvažovať napríklad ich úhrn. V praxi si predstavíme zjednodušenú prípadovú štúdiu:

Každý sa na pár minút zahrá na poistného matematika v malej krajinke s 10 000 obyvateľmi. Keďže krajinka vznikla nedávno, všetci jej obyvatelia sú ekonomicky aktívni – odvádzajú peniaze na dôchodkové sporenie! Takto každý z nich musí odvádzať ešte 40 rokov istú čiastku, ktorú my ako ministri krajinky potrebujeme odhadnúť!

Zistime odhad množstva ľudí, ktorí o 40 rokov budú poberať dôchodok. Keďže naši spoluobčania musia tvrdo pracovať, aby našu maličkú ostrovnú krajinku postavili na nohy, povedzme že ich pravdepodobnosť dovŕšenia dôchodkového veku je 0.6.  To znamená, že štyria z desiatich sa dôchodku nedožijú a preto odvádzali peniaze nadarmo!

Dostaneme 10 000 náhodných veličín z Alternatívneho rozdelenia a nás zaujíma úhrn, t.j. množstvo budúcich dôchodcov o 40 rokov! Táto štatistika je už samozrejme Binomicky rozdelená a na základe Moivreovej-Laplaceovej vety pri veľkom počte ľudí môžeme tvrdiť, že: Ak sa ešte pamätáte na normovanie, potom nasledujúci kľúčový vzorec pre vás nebude problém pochopiť: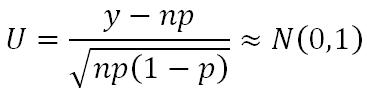

Výsledok zobrazuje nasledujúci obrázok:

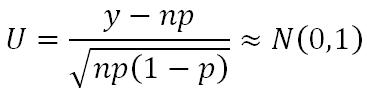
Vzhľadom k takmer identickej podobe (použil som priehľadný typ dátovej čiary - vidieť tmavé sfarbenie binomického rozdelenia) môžeme hravo použiť pri výpočte očakávaného počtu dôchodcov Normálne rozdelenie. Problém výpočtu sumy, ktorú budú musieť spoluobčania platiť po dobu 40 rokov necháme pre ozajstných poistných matematikov a našu hru ukončíme . 

Lindeberg – Lévy

Táto tzv. zovšeobecnená verzia predchádzajúcej uvažuje akéhokoľvek rozdelenie  (identicky rozdelené a nezávislé náhodné veličiny). V tomto prípade musíme vedieť odvodiť konečnú strednú hodnotu a rozptyl.

 

Pamätajte na dôležitú vec! Pri manipulácii s normovaním je potrebné disponovať veľkým výberovým súborom (číslo n).

V prípade nesplnenia dostatočnej veľkosti hrozí, že váš prieskum nebude mať kvalitnú vypovedaciu schopnosť. Z hľadiska opodstatnenia veľkosti výberového súboru vám postačí nazrieť späť na prvý obrázok s ilustráciou Poissonovho a Binomického rozdelenia.

Budúci článok budeme rozoberať dôležitosť log–normálneho rozdelenia a taktiež prvýkrát použijeme dáta z reality (ceny burzovo obchodovaného titulu).