Normálne rozdelenie - 1.diel

 

Toto, štatisticky významné rozdelenie je tak dôležité, že sa mu budem venovať vo viacerých dieloch.

Už pri popise charakteristík náhodných veličín som ho spomenul v súvislosti so špicatosťou a šikmosťou. Ak si nájdete pojmy ako regresná analýza, alebo chcete modelovať úrokové miery, ceny finančných derivátov apod., všade sa stretnete so základom (axióm) normálne alebo log-normálne rozdelenej veličiny, ktorú mienite analyzovať.

Otázka splnenia normálnosti veličiny je už odlišná kapitola, ktorá sa rieši individuálnymi testami tzv. normality, poprípade sa používajú sofistikovanejšie modely s použitím napríklad Študentovho rozdelenia.

Jednorozmerné normálne rozdelenie vyzerá takto:

V Excel-i (viď sample file) si ho môžeme vygenerovať nasledovne:
1) Nadefinujte strednú hodnotu µ a smerodajnú odchýlku δ
2) zvoľte si interval hodnôt X, so stredom rovným µ a rozpätím rovným aspoň 3δ
3) Vedľa v novom stĺpci použijeme funkciu norm.dist:
=NORM.DIST(hodnota X;Priemer - stredná hodnota; Smerodajná odchýlka;1-Kumulovaná distr. a 0- pravdepodobnostná funkcia)
Výsledok si môžete zobraziť do grafu napríklad takto:

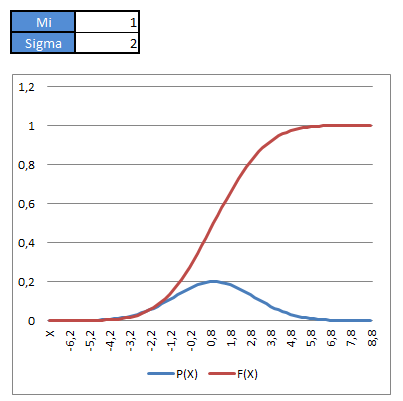
Modro sfarbená funkcia je pravdepodobnostné rozdelenie (symetrické okolo strednej hodnoty) a bordová je distribučná funkcia, ktorá evidentne konverguje k hodnote 1. Závislosť “ostrosti” pravdepodobnostnej funkcie a tiež uhol rastu distribučnej funkcie spravidla závisí na veľkosti rozptylu (smerodajnej odchýlky).

Platí: čím menší rozptyl, tým je rozdelenie náhodnej veličiny presnejšie, kopec je strmší a spád distribučnej funkcie väčší.

Pokračujme definíciou momentovej vytvárajúcej funkcie. Najprv pre náhodnú veličinu X a potom z nej odvodíme momentovú funkciu pre normovanú Y:

 

 

 

 

 

 

 

Prečo sme vlastne použili normovanú veličinu Y? Lebo uvažovaná veličina X má normované normálne rozdelenie s nulovou strednou hodnotou a rozptylom rovným 1.

Ak chceme z normálne rozdelenej veličiny utvoriť normovanú normálne rozdelenú veličinu, použijeme:

Tento vzťah je veľmi užitočný, bez ktorého sa ťažko riešia problémy v praxi. Takže ho doporučujem ovládať .  V rámci článku by bolo vhodné uviesť charakteristiky rozdelenia, tie však nebudem odvodzovať, nakoľko sa jedná o ten istý princíp ako v predchádzajúcich rozdeleniach, takže:

To by bolo pre dnešok všetko. Vyzerá to byť náročnejšie na mozgové bunky, no pri riešení praktických problémov sa relatívne často používa štatistika, teda človek potrebuje definovať to, ako sa správa pravdepodobnosť (definovať rozdelenie) a na základe charakteru pravdepodobnosti môže predpovedať a rozhodovať. O to lepšie sa ľuďom manipuluje s dátami a problematikou, ak dokážu posúdiť ktoré rozdelenie je vhodné a ktoré nie!

Nemusíte si pamätať vzorčeky, stačí ak sa na ne pozriete a viete podstatu! Prakticky stačí, ak poznáte momentovú funkciu, z ktorej dokážete nadefinovať čokoľvek!