Histogram
Tento názov by pre väčšinu “ekonómov” alebo ľudí, ktorí sú v kontakte s analýzou dát nemal byť neznámy pojem. Skoro by som bol zabudol, sample file je taktiež k dispozícii. Každopádne 
tí, ktorí ho vidia po prvýkrát na obrázku si položia otázku: Prečo individuálny názov pre v podstate stĺpcový graf? Je potreba vôbec rozlišovať medzi stĺpcovým grafom a Histogramom? Odpoveď znie, ÁNO. Ak si spomeniete na to, ako som sa zaoberal náhodnými veličinami, tak som sa nevenoval typom náhodných veličín. V každom prípade poznáme Spojité a Nespojité typy. Spojité náhodné veličiny nadobúdajú (štatisticky) izolovanú hodnotu s nulovou pravdepodobnosťou (nedá sa načapovať presne 1,00… litrov piva). Nespojité sú charakterizované práve izolovanými hodnotami (vašu web stránku nemohlo navštíviť 0,98765…. návštevníkov, ale 1 alebo 2 alebo n). Ale ak vaša stránka je napríklad Facebook a vy sledujete návštevnosť v sekundách, v štatistike môžeme zobrať v úvahu fakt, že tieto celkom pozoruhodne meniace sa izolované hodnoty návštevnosti v tak krátkom čase sa správajú skoro ako spojité. Práve preto si štatistici povedali, že túto “spojitosť” sa budú snažiť vyjadriť stĺpcovým grafom, v ktorom sa jednotlivé stĺpce dotýkajú, čo znamená niečo ako kvázi spojenie skupín. Slovo skupín som použil preto, lebo hodnoty histogramu nie sú len tak zbežné! Histogram totiž zobrazuje skupinovú početnosť!
tí, ktorí ho vidia po prvýkrát na obrázku si položia otázku: Prečo individuálny názov pre v podstate stĺpcový graf? Je potreba vôbec rozlišovať medzi stĺpcovým grafom a Histogramom? Odpoveď znie, ÁNO. Ak si spomeniete na to, ako som sa zaoberal náhodnými veličinami, tak som sa nevenoval typom náhodných veličín. V každom prípade poznáme Spojité a Nespojité typy. Spojité náhodné veličiny nadobúdajú (štatisticky) izolovanú hodnotu s nulovou pravdepodobnosťou (nedá sa načapovať presne 1,00… litrov piva). Nespojité sú charakterizované práve izolovanými hodnotami (vašu web stránku nemohlo navštíviť 0,98765…. návštevníkov, ale 1 alebo 2 alebo n). Ale ak vaša stránka je napríklad Facebook a vy sledujete návštevnosť v sekundách, v štatistike môžeme zobrať v úvahu fakt, že tieto celkom pozoruhodne meniace sa izolované hodnoty návštevnosti v tak krátkom čase sa správajú skoro ako spojité. Práve preto si štatistici povedali, že túto “spojitosť” sa budú snažiť vyjadriť stĺpcovým grafom, v ktorom sa jednotlivé stĺpce dotýkajú, čo znamená niečo ako kvázi spojenie skupín. Slovo skupín som použil preto, lebo hodnoty histogramu nie sú len tak zbežné! Histogram totiž zobrazuje skupinovú početnosť! Predstavme si situáciu, keď máme 14 rôznych dlžníkov s konkrétnymi dlžnými čiastkami. My by sme chceli ich istým spôsobom rozdeliť do skupín a taktiež získať prehľad o naše
j “úžerníckej” činnosti. 
Použijeme na to Histogram. Podľa pridanej tabuľky doplníme hranice tried Prejdime na kartu Data a možnosť Analýza dat a vyberieme si Histogram (V prípade, ak takúto možnosť nemáte, musíte si pridať tzv. Add-in nástroj, viď prvý článok). V následne zvolenom dialógovom okne si nadefinujeme Vstupní oblast, Hranice tříd, potom Výstupní oblast. Taktiež zaškrtneme Kumulatívni procentuální podíl a Vytvořit graf. Výsledok sa nám zjaví vo forme tabuľka a grafu. 
j “úžerníckej” činnosti. 
Použijeme na to Histogram. Podľa pridanej tabuľky doplníme hranice tried Prejdime na kartu Data a možnosť Analýza dat a vyberieme si Histogram (V prípade, ak takúto možnosť nemáte, musíte si pridať tzv. Add-in nástroj, viď prvý článok). V následne zvolenom dialógovom okne si nadefinujeme Vstupní oblast, Hranice tříd, potom Výstupní oblast. Taktiež zaškrtneme Kumulatívni procentuální podíl a Vytvořit graf. Výsledok sa nám zjaví vo forme tabuľka a grafu. 
Pre estetické cítenie som si upravil tabuľku do formátu, aký má tabuľka skupiny a taktiež som upravil hrúbku dátových stĺpcov na grafe. Kliknite na stĺpce v grafe tak aby sa označili, pravým tlačidlom Format data series… a v možnosti Gap Width priblížte kurzor k hodnote No Gap približne na 8% (aby medzi stĺpcami nebol tak dramatický gap).
Interpretácia grafu: na vodorovnej osi máme naše skupiny, vertikálna os na ľavej strane zobrazuje počet prvkov jednotlivých skupín. Pravá strana vertikálnej osi zobrazuje kumulatívne percento jednotlivých skupín ( prvá skupina mala 14,29%, druhá 14,29%+21,42% = 35,71% – spolu obidve skupiny, atď.). Kumulatívne percento je graficky znázornené bordovou čiarou, všimnite si, že posledná skupina vždy nadobúda hodnotu 100%.
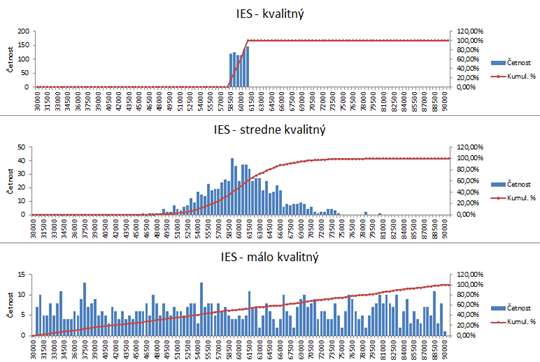
Vráťme sa k našim typom IES platových skupín,z predchádzajúceho článku. Vytvorme si histogramy, pre každý z nich! Triedy si pri tvorbe histogramov musíte vždy premyslieť! Vezmite v úhavu tvar grafu, minimá a maximá alebo iné charakteristiky polohy (viď. predchádzajúci článok). V tomto prípade by bolo vhodné si vytvoriť triedy s počiatočnou hodnotou 30000Kč, pričom každá ďalšia je väčšia o 500Kč až po maximum 90000Kč. Výsledky si môžete premiestniť na spoločný graf a mierne upraviť napríklad takto:
Bordové čiary vyjadrujú niečo ako Empirickú Distribučnú funkciu a Modré stĺpčeky Empirickú Hustotu pravdepodobnosti! O čo sa vlastne jedná??? Principiálne ide o to, že v štatistike chceme náhodnú veličinu charakterizovať, teda dozvedieť sa o nej čo najviac, aby sme vedeli predpokladať jej správanie sa a tým pádom aj vyvodiť dôsledky rozhodovania sa. Ako v našom príklade s platmi, snažíme sa čo najlepšie popísať jednotlivé typy IES – škôl tak, aby sme sa rozhodli, na ktorú ísť študovať alebo nie, taktiež pozrieť sa na zúbok VŠE fakultám a uistiť sa v rozhodnutí! Uznajme, že štúdium na IES – málo kvalitný by nebolo celkom rozumné, nakoľko nepatríme k študentom, ktorí by sa šprtali v knihách 12hod. denne a na druhej strane nechceme po štúdiu dostávať na výplatnej páske hodnotu približne 30 000Kč, ktorá je dosť možná! Lepšie by sme urobili, ak by sme si vyštudovali IES-kvalitný s akou takou garanciou platov s rozmedzí 57 000 až 61 000Kč.
A práve okrem základných polohových charakteristík nás zaujíma aj tvar rozdelenia pravdepodobnosti. Lebo celý čas tu v podstate hovoríme o pravdepodobnostiach! Zatiaľ empirických. Tak napríklad empirická pravdepodobnosť, že po IES-kvalitný budem zarábať 84 000Kč je nulová, zatiaľ čo paradoxne u IES-stredne a málo kvalitný to paradoxne neplatí!!!
Tu sa nám žiada položiť si otázku, koľko chcem v budúcnosti mať príjem! Hneď po tom nasleduje otázka, s akou pravdepodobnosťou budem tento príjem zarábať??? Práve v takýchto prípadoch nám len jednotlivé charakteristiky polohy a variability nebudú stačiť! My totižto podľa Hustoty a Distribučnej funkcie dokážeme na danú pravdepodobnostnú otázku odpovedať!!!
Obecne sa začíname baviť o tzv. rozdelení pravdepodobnosti. Jedná sa spôsob, akým výsledkom - náhodným javom môžeme priradiť priradiť pravdepodobnosti! To znamená, interval od 0 do 1 musíme rozrezať na malé kúsky, priradiť jednotlivým platom (náhodným javom), poprípade platovým kategóriám a to všetko na rozhraní absolventských platov školy napríklad IES – kvalitný (náhodná veličina)!
To sme v podstate empiricky urobili! Každý modrý stĺpček nám vyjadruje absolútny výskyt náhodného javu. To znamená, že ak každú hodnotu stĺpčeka predelíme množstvom všetkých absolventov danej školy, dostaneme relatívnu početnosť, ktorá sa rovná pravdepodobnosti výskytu! Vezmime v úvahu úvodný histogram a predeľme počty dlžníkov v jednotlivých skupinách celkovým počtom všetkých, čo nám dĺžia a uvidíte čo sa stane!
Všimnime si, že sa nám ľavá vertikálna os tak trošku pozmenila. Namiesto počtov výskytov máme ich relatívne početnosti, tým pádom empirické pravdepodobnosti ich výskytu! Teraz máte možnosť vidieť empirickú Hustotu a Distribučnú funkciu v pravom slova zmysle!
Prenesme sa z empírie do teórie! Komu by sa chcelo pri každej analýze platov IES škôl strácať čas empirickým zisťovaním “tvaru” náhodnej veličiny??? Mne rozhodne nie a taktiež mnohým štatistikom! Ak porovnáme teoretické pravdepodobnostné rozdelenie (Hustota a Distribučná funkcia - tvar) s empirickým (Histogram) a zistíme, že sa len veľmi slabo odlišujú, stačí používať tieto teoretické pravdepodobnostné rozdelenia a tým pádom odhadovať ich parametre a máme postarané prakticky skoro o všetko (túto podobnosť empírie a teórie je potreba testovať).
Porovnajme si IES-stredne kvalitný s Normálnym rozdelením!
Na základe dodatočných testov (budeme rozoberať neskôr) môžeme aproximovať empirickú distribučnú funkciu a hustotu (empirické rozdelenie) Normálnym rozdelením, ktorého hustotu, distribučnú funkciu a taktiež charakteristiky hravo dokážeme spočítať!
V ďalšom článku sa budeme venovať charakteristikám variability a šikmosti a špicatosti.
Žiadne komentáre:
Zverejnenie komentára