Chodíte radi nakupovať a nepoznáte Binomické rozdelenie? Potom je na čase, aby ste sa s nim oboznámili! Ako ste si už určite zvykli, sample file je opäť k dispozícii, takže po stiahnutí môžeme pekne začať príkladom.
Predstavte si svoj obľúbený obchod, do ktorého zavítate vždy, ak máte chuť utratiť zopár €. Elektronika, oblečenie, topánky, kabelky, v podstate je to jedno. Každý obchod tvorí určitý marketing, aby si budoval klientelu.
Predstavme si, že dostaneme 5000€, ktoré máme v priebehu nasledujúceho mesiaca rozdať ľuďom vo forme darčekových poukážok tak, aby sme oslovili tých s najväčšou lojalitou!
Niektorí z vás si povedia, čo je na tom tak zložité – vezmem a rozdám každému, kto navštívi obchod a zopár € tam utratí. No v skutočnosti to vyzerá tak, že zdanlivo minorita zákazníkov permanentne vytvára majoritnú časť tržby! Chceme azda peniaze rozdať tým, ktorí utrácajú len ak sú výpredaje a diskonty? Nie! Chceme sa odvďačiť tým, ktorí si poctivo aktualizujú šatník a sú zdravými piliermi brandu. Vráťme sa k našim 5000€ a kvázi investičnej úlohe. Investičná v zmysle – ak oslovíte lojálneho zákazníka, ten v skutočnosti utratí omnoho viac, než by sme si dokázali predstaviť, on je povedzme dojná kravička nášho biznisu.
Ako ich vyselektovať? Sú na to rôzne spôsoby z oblasti dataminingu a štatistických metód, ktoré nie sú lacná záležitosť avšak retailovo orientovaná spoločnosť sa v dnešnej dobre bez nich nezaobíde. Povedzme, že sme na základe regresnej analýzy určili tri možné scenáre počtu nakupujúcich pre budúci mesiac:
Vezmime si údaje o nákupoch za posledné tri mesiace a zistíme, že množstvo ľudí, ktorí utrácajú sa zvyšuje s príchodom leta (Máj – 72, Jún – 85, Júl –96). Výstup z externého dataminingového modelu hovorí ,že ľudia, ktorých platby presahujú hranicu 60€ sú cieľová skupina, skupina na ktorú je potreba cieľovať kupóny, zľavy benefity a iné nástroje komunikácie.
Z disponibilných štatistík za posledné tri mesiace zistíme relatívnu početnosť ľudí, ktorí utratili viac ako 60€. Použijeme funkciu =COUNTIF(B3:B98;">60")/COUNT(B3:B98).
Tieto relatívne početnosti budeme používať v modeli binomického rozdelenia, ktoré vyzerá takto:
V danej pravdepodobnostnej funkcii používame relatívnu početnosť p ako odhad pravdepodobnosti výskytu javu. Použiteľný vzorec bude vyzerať nasledovne:
A v Exceli máme funkciu =BINOM.DIST(Počet úspechov;Počet všetkých pokusov;p;0-pravdepodobnosť alebo 1-distribučná funkcia), ktorá počíta pravdepodobnosť výskytu javu, resp. kumulovanú pravdepodobnosť.
Stredná hodnota a rozptyl rozdelenia vyzerajú nasledovne:
Nasledujúca tabuľka nám ukáže hodnoty pravdepodobnosti, že náhodný kupujúci v obchode dostane zľavu, plus očakávaný počet takýchto šťastlivcov spolu so smerodajnou odchýlkou.
Ako nasledujúce dáta môžeme použiť? Zatiaľ sme nehovorili o veľkosti zľavy, resp. ako rozdeliť tých 5000€ pre skupinu vyvolených! V tomto prípade musíme byť opatrní, nemôžeme prehliadnuť rozpočet!!! Použijeme dva prístupy.
Prvý: odhadneme počty bonusových zákazníkov pomocou súčtu strednej hodnoty a smerodajnej odchýlky. Následne predelíme rozpočet množstvom očakávaných ľudí.
Druhý: pomocou funkcie =BINOM.INV(počet pokusov;p;0,95) vypočítame množstvo prípadov, pre ktoré by binomicky rozdelený náhodný jav mal nastať s pravdepodobnosťou 0.95 (interval spoľahlivosti). Tieto hodnoty taktiež použijeme na predelenie rozpočtu a výsledok je k dispozícii tu:
V našom prípade, kedy potrebujeme byť maximálne opatrní, vyberieme si ten najpriaznivejší scenár o počte zákazníkov, takže obmedzíme výšku bonusového kupónu na 60€. Úloha tvorby benefičných programov a celkovo vernostných stratégií je enormne citlivá problematika. Je preto nevyhnutné jej venovať dostatok pozornosti a HLAVNE používať sofistikované štatistické prístupy.
V nasledujúcom diele si ešte ukážeme ostatné charakteristiky a taktiež vzhľad binomického rozdelenia.


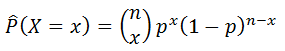


Žiadne komentáre:
Zverejnenie komentára