Šikmosť a špicatosť
Tieto charakteristiky bude tak trocha problematické vysvetliť, nakoľko sme si nedefinovali jedno z asi najviac skloňovaných pravdepodobnostných rozdelení: Normálne rozdelenie. Zatiaľ si ukážeme iba postup, ako takéto rozdelenie modelovať! Stiahnite si prosím nový sample file a môžeme začať.
V prvom rade si musíme nagenerovať hodnoty náhodnej veličiny od -4 do 4 s
absolútnym prírastom 0.01. Tieto hodnoty dostaneme napríklad tým, že do bunky A2 vložíme hodnotu –4 a v A3 bunke napíšeme vzorec =A2+0,01. Tento vzorec skopírujeme a vložíme do oblasti od A3 do A802. Tento stĺpec si označíme ako x a potom sa budeme v ďalšom stĺpci f(x) zaoberať nasledujúcou hustotou pravdepodobnosti:
Daný vzorec môžeme napísať takto: =(1/POWER(2*PI();0,5))*EXP(1)^(-0,5*(A3^2)), kde pomocou funkcie POWER vytvoríme odmocninu, PI() je zase Ludolfovo číslo a EXP(1) pre zmenu Eulerovo. Následne sa pokúsime z vytvorených stĺpcov vytvoriť graf (Scatter) a výsledok by mal vyzerať nasledovne:
Tento typ rozdelenia sa tiež nazýva normované normálne rozdelenie, ktoré je charakteristické tým, že jeho stredná hodnota je rovná 0, rozptyl je rovný 1, šikmosť a špicatosť 0. A práve pomocou tohto normovaného rozdelenia sa riadia charakteristiky šikmosti a špicatosti.
Pri týchto charakteristikách je potrebné zaviesť pojem NORMOVANIE. Jedná sa spravidla o štatistiku, v ktorej od hodnoty X odčítame jej strednú hodnotu E(X) a potom celý výraz predelíme smerodajnou odchýlkou.
Táto veličina sa v literatúre zvykne označovať písmenom U. Tento proces normovania využijeme pri výstavbe momentových charakteristík:
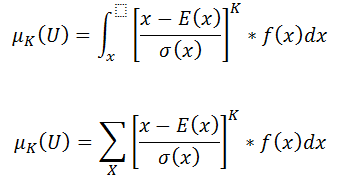
Ako iste tušíte, výraz s integrálom je popis momentovej charakteristiky pri spojitých veličinách a druhý zo sumou pre nespojité veličiny. Nás budú zaujímať momenty: Tretí (šikmosť) a štvrtý (špicatosť). Tým pádom šikmosť môžeme matematicky zapísať ako:
Táto štatistika nám ukazuje, do ktorej strany sa zobrazuje prevažná časť prípadov v rozdelení, teda či je zošikmená doprava alebo doľava. Pre špicatosť samozrejme platí:
Číslo –3 som použil v rámci zaužívaného postupu, ktorý sa odkazuje na hodnotu normovaného normálneho rozdelenia, ktorého špicatosť je rovná 3. Takto sa štatistika nazýva koeficient špicatosti a primárne porovnáva špicatosť (hrot histogramu) dátového súboru hodnôt s týmto štandardným rozdelením.
Pre ilustráciu si urobíme taký malý pokus. Vygenerujeme si tri premenné s 20000 hodnotami normovaného normálneho rozdelenia a vypočítame si všetky základné charakteristiky. Pre výpočet šikmosti použijeme funkciu =SKEW(), kde v zátvorke označíme výberový súbor. Analogicky pre špicatosť použijeme funkciu =KURT().
Ak vychádzame z toho, že poznáme rozdelenie, z ktorého boli hodnoty vygenerované, vieme veľmi dobre, že stredná hodnota (priemer je v tomto prípade nestranný odhad) má byť rovná 0. Pre rozptyl platí teoretická hodnota rovná 1 a šikmosť spolu so špicatosťou má byť rovná 0.
TOTO je PRÍKLAD toho, AKO sa ODLIŠUJÚ teoretické HODNOTY od EMPIRICKÝCH! Nabudúce si budeme ukazovať zopár zaujímavých rozdelení náhodných veličín.
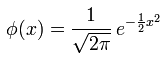
Žiadne komentáre:
Zverejnenie komentára