Som veľmi rád, že sa pomaly a isto dostávame k tematickému koncu a preto nebudem chodiť okolo horúcej kaše a začnem.
Pamätáte sa na pojem Normovanie? Ak nie skúste listovať v pamäti alebo v skôr narodených článkoch, pre nedočkavých stačí kliknúť na slovo Normovanie.
Spomeniem fakt, že normovaná veličina Ui je normálne rozdelená s parametrami:
Ľudské potreby sú však nevyspytateľné, obzvlášť v pitvaní sa v dátach čo viedlo k poznávaniu nasledujúcej štatistiky:
Využíva sa v rôznych oblastiach, ako príklad spomeniem testovanie závislosti kategoriálnych premenných v kontingenčnej tabuľke. Prejdime k hustote pravdepodobnosti:
V tomto prípade máme zadanú podmienku prirodzeného čísla pre chí-kvadrát štatistiku. V prípade nesplnenia podmienky je hustota rovná nule.
Momentová vytvárajúca funkcia spolu so základnými charakteristikami vyzerá nasledovne:
Tým pádom vám už nič nebráni k tomu, aby ste si stiahli sample file a pozreli si model rozdelenia a použité vzorčeky:
Ako ste si určite všimli, pre modelovanie som nepoužil žiadnu funkciu, ktorá by pripomínala pojem Chí kvadrát ale Gama rozdelenie! Ja som Vám totiž zatajoval celkom dôležitý fakt:
Chí kvadrát rozdelenie je konkrétny typ Gama rozdelenia, pre ktoré platí:
Vďaka tomuto poznatku som mohol namodelovať rozdelenie nasledovne:
Hustota pravdepodobnosti:
=GAMMADIST($D$2;$B$2;2;FALSE) =GAMMADIST( X ; v/2 ; 2 ; FALSE )
Distribučná funkcia:
=GAMMADIST($D$2;$B$2;2;TRUE) =GAMMADIST( X ; v/2 ; 2 ; TRUE )
Aby ste nepovedali, že som skúpy na informácie, prezradím vám ďalší vylepšovák: Ak je ν (tiež sa nazýva stupeň voľnosti) dostatočne veľké, povedzme že väčšie ako 30, môžeme aj toto rozdelenie definovať tzv. Fischerovou aproximáciou:
Kde up je kvantil normovaného normálneho rozdelenia. Na záver článku a taktiež tematického celku by som chcel ako bonus pridať súbor, ktorý som vypracoval v rámci úlohy o Weibullovom rozdelení (mal príjemne pozitívnu odozvu). V ňom samozrejme nezabudnite povoliť makra a ak sa dostanete do VBA prostredia (Alt + F11), môžu vám základné makra poslúžiť ako inšpirácia.
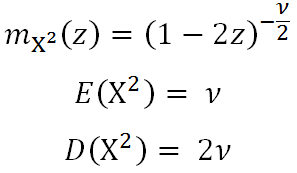
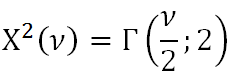
Žiadne komentáre:
Zverejnenie komentára