Charakteristiky náhodnej veličiny (3.diel)

 

Milí čitatelia! Dostávame sa do fázy, teda lepšie povedané ja som sa ocitol vo fáze, keď musím dôrazne porozmýšľať o tom, čo som vám v rámci náhodných veličín povedal a čo ešte nie. Dokážeme rozlišovať stochastické javy od deterministických. Taktiež zamyslieť sa nad jednotlivými náhodnými veličinami. Používať histogramy a nezabúdajme na to, že priemer niekedy nemusí bezprostredne poskytovať informáciu, ktorú potrebujeme.

Charakteristiky variability

Variabilita ako pojem by sa ľudským spôsobom dala definovať ako sklon k vychýleniu sa od očakávanej hodnoty. Predstavme si situáciu, v ktorej máme naše známe tri typy IES škôl a rozhodujeme sa, na ktorú z nich nastúpiť. Aplikácia kvartilov nám ako tak pomohla vybrať si a to zobrazením študentov, ktorí zarábajú relatívne málo alebo relatívne veľa v porovnaní so strednou hodnotou!

Už momentové charakteristiky nám hovorili niečo o variabilite nástupných platov, kde IES-kvalitný škola mala nízku variabilitu a tým pádom jej absolvent má štatistickú istotu, že jeho cifra na výplatnej páske sa bude pohybovať v okolí priemernej mzdy. Toto tvrdenie neplatí pre študentov IES-nekvalitný! Takýto absolvent je elastický a platí pre neho jednoduché pravidlo: učí a pracuje na sebe, tým pádom zarobí nemalé peniaze; ak je lenivý a učí sa iba pre titul bude poberať smiešne peniaze!

V praxi sa však používa charakteristika, nazývajúca sa rozptyl, spolu s jej odmocninou – smerodajnou odchýlkou.

Rozptyl a Smerodajná odchýlka

Táto charakteristika sa vyjadruje obecne v tvare:

Alebo môžeme použiť výpočtový tvar:

Sami vidíte, že sa rovná súčtu štvorcov odchýlok hodnôt od strednej hodnoty. Ako každú inú štatistiku, aj táto má svoj (pre daný výberový súbor ) špecifický výpočtový tvar. Do hry v tomto prípade vstupuje stredná hodnota. Ak by sme napríklad vedeli ,že výberové hodnoty pochádzajú, alebo sa približne podobajú normálnemu rozdeleniu, môžeme strednú hodnotu nahradiť nestranným odhadom – aritmetickým priemerom a empirický vzorec pre rozptyl by vyzeral takto: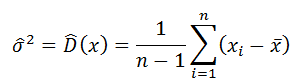

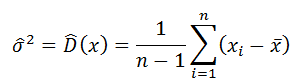
V prípade, že pracujete s veľkým množstvom hodnôt, stáva sa že sa vzorec zjednoduší a to tak, že v menovateli bude iba počet hodnôt:

Stiahnime si sample file, tí ktorí používali súbor z predchádzajúceho článku, majú o starosť menej. Excel poskytuje viacero možností výpočtu rozptylu:

 

Asi najviac používanými funkciami sú VAR a VARP. Pričom VAR nám vypočíta výberový rozptyl (posledný vzorec) a VARP sa pokúša vyhodiť hodnotu rozptylu pre celú populáciu. Logika vzorcov je jednoduchá, stačí označiť oblasť buniek, z ktorej chceme rozptyl. V prípade potreby smerodajnej odchýlky nám stačí urobiť odmocninu z rozptylov alebo analogicky použiť vzorce pre výpočty:

Aj v tomto prípade je analógia výpočtu jednoduchá - totožná s rozptylom. My použijeme funkcie STDEV a STDEVP. Výsledky variability budeme komentovať z nasledujúcej tabuľky:

Tieto výsledky len potvrdzujú to, čo nám predpovedali kvartily. Tým pádom už určite chápete, prečo som IES-kvalitný nazval kvalitný súbor absolventov apod.. Otázkou znie, prečo vlastne počítame rozptyl a smerodajnú odchýlku? A prečo to vôbec všetko robíme cez mocniny, keď nám hravo postačí súčet absolútnych hodnôt diferencií?

Smerodajná odchýlka slúži predovšetkým na pohodlnú interpretáciu (hodnoty indikujú, o koľko sa navzájom líšia výplatné pásky absolventov) a rozptyl zohráva dôležitú výpočtovú úlohu v komplexnejších štatistických výpočtoch. Riešiť absolútne diferencie nie je bezprostredne zlá cesta, no všestrannejšie sú štvorcové výpočty.

Budúcim článkom dokončíme charakteristiky náhodných veličín a rozoberieme si niektoré potrebné pravdepodobnostné rozdelenia.