Logaritmicko-normálne rozdelenie

 

Na úvod začneme burzou. Ukážeme si, v akom zmysle má Logaritmicko-normálne rozdelenie význam. No na začiatok by sme potrebovali dáta.

Navštívime stránku http://www.google.com/finance v ktorej si nájdeme titul ľubovoľnej akcie. Ja som si zvolil Ford Motor Company:

Klikneme na Historical prices a potom stiahneme historické ceny do súboru v Excel-i. Dáta sa uložili do formátu .csv tým pádom si ich musíme spracovať do použiteľnej podoby. Použijeme možnosť Text-To-Columns, ktorý som opísal v jednom z úvodných článkov. Ďalej môžeme vymazať všetky stĺpce okrem Close. Všimnime si dôležitý poznatok, t.j. hodnoty sú uložené ako dátum! Je to dosť nepríjemná záležitosť a my potrebujeme mať hodnoty vo formáte číslo s oddeľovačom desatinných miest čiarkou!

Ako na to?

1) stĺpec Close skopírujeme do Word súboru a nahradíme znak bodka - “ . “ čiarkou - “,”

2) potom dáta z Word-u skopírujeme späť do Excel-u a upravíme ich na formát číslo

 

Tento “prenos” do Word súboru odporúčam urobiť v zmysle zbavenia sa formátu ako dátumu. Takto prenesené dáta sú v podstate kľúčové hodnoty, v ktorých stačí urobiť náhradu bodky čiarkou (Ak by sme sa pokúsili nahradzovať v Excel-i, dostali by sme nežiaduci formát: dd,mm,rrrr). Výsledná časová rada by mala vyzerať nasledovne:

Takto ošetrené dáta sú pripravené na analýzu! Pomocou histogramu si môžeme analyzovať charakter časovej rady. Budeme sa snažiť priblížiť tvaru normálneho rozdelenia. V nasledujúcom obrázku budete mať náhľad histogramov pre pôvodnú časovú radu, potom pre  medzi-denný koeficient rastu a nakoniec logaritmická transformácia daného koeficientu(viď sample file).

Nakoľko sa svetlo-sfarbené histogramy podobajú, vhodnejšie je uvažovať transformáciu logaritmom z dôvodu nižšieho rozptylu ale hlavne:

Tým pádom môžeme konštatovať, že náhodná veličina ln(Y) má normálne rozdelenie. Otázka však znie, aké rozdelenie bude mať veličina Y ? Odpoveď znie Logaritmicko-normálne a spôsob, akým ho môžeme odvodiť je pomocou tzv. funkcie náhodných veličín!  Nakoľko sa jedná o celkom obsiahly proces, nebudem ho rozpitvávať, len uvediem dôležitý predpoklad:

Funkcia musí byť spojitého/hladkého charakteru pre celý definičný obor (existuje derivácia)!

Naša funkcia logaritmu je hladká v intervale nezáporných čísel (koeficient rastu je vždy kladné číslo). Vďaka tomu bude rozdelenie veličiny Y –> koeficient rastu (základná štatistika pri časových radách) vyzerať nasledovne:

Takto vytvorené rozdelenie má nasledujúce charakteristiky polohy a variability:

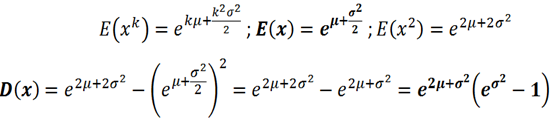
Pamätajte, hodnoty µ a δ² sú stredná hodnota a rozptyl pre veličinu ln(X), ktorá je normálne rozdelená. Avšak ak budeme uvažovať len veličinu Y, vyššie uvedené charakteristiky pre ňu platia ako log-normálne rozdelenú. Na budúce si namodelujeme log-normálne rozdelenie na základe stiahnutých dát.