Testovanie hypotéz

 

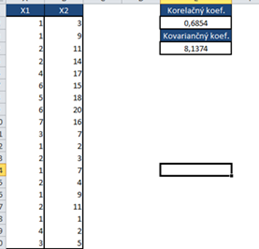
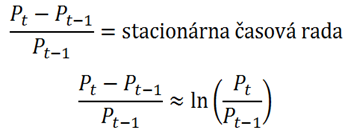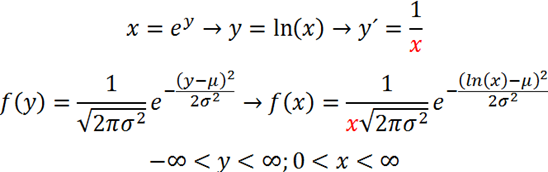Po dlhodobom vysvetľovaní pravdepodobnostných rozdelení by nebolo na škodu definovať, kde v praxi sa tieto poznatky dajú využiť.

To je hlavný dôvod, prečo som začal písať o testovaní hypotéz! V praxi sa určite stretnete s otázkami typu:

Ako to bude vyzerať v budúcnosti? Čo môžeme očakávať? S čím máme počítať? …

Keďže nikto z nás nevlastní magickú guľu, ktorá nám ukáže budúcnosť, neostáva nám nič iné ako spoliehať sa na predpoklady, teda odhadovať! V tejto situácii si musíme vystačiť s tým čo máme: poznatkami z minulosti!

Dôvod? – Na základe minulosti dokážeme kvantifikovať kľúčové premenné, definujúce náš problém a zároveň určiť vzťah medzi nimi!

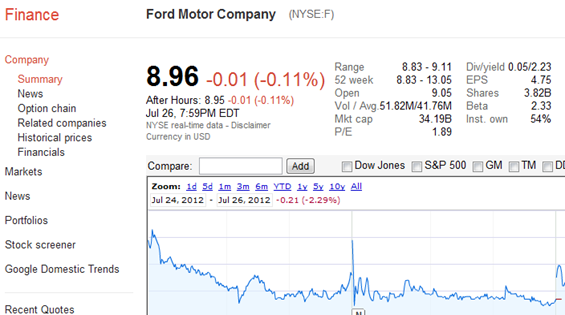
Ako ilustráciu by som uviedol plantážnika, ktorý spracúva kokaín. My vieme, že jeho plantáž má isté kapacity a výstup - úrodu! Na základe pozorovania dokážeme popísať výrobné možnosti plantáže!

Potom nastane situácia, že ho kontaktuje veľkoodberateľ a chce s ním dohodnúť kontrakt na isté množstvo kíl za určitú časovú jednotku (200 Kg mesačne) a cenu.

Otázka znie, či spracovateľ si môže dovoliť uzavrieť takýto obchod, resp. čo by urobil veľkoodberateľ ak by za svoje peniaze nedostal to čo chce??? Reklamoval by to? Sťažoval sa na Zväze ochrany spotrebiteľov? V tomto štádiu si každý môžete predstaviť vlastný scenár, no zhodneme sa, že by sme sa nechceli ocitnúť v takej situácii!

Týmto som chcel demonštrovať fakt, že testovanie hypotéz sa využíva všade – aj v zmienenom priemysle by malo opodstatnenie ak by niekto ovládal štatistiku

Ako delíme hypotézy?

Parametrické testy vyšetrujú jednotlivé parametre rozdelenia (stredná hodnota – očakávané množstvo vyprodukovaného kokaínu; rozptyl – volatilita jeho produkcie apod..)

Neparametrické testy trápi problematika tvaru rozdelenia, závislosti premenných a iné.

Čo potrebujeme sformulovať?

1) musíme si nadefinovať predpoklad – nulovú hypotézu H₀ (očakávaná mesačná dodávka kokaínu je 100 Kg)

2) potrebujeme si položiť otázku typu: čo ak…? teda alternatívnu hypotézu H₁

- Tá môže byť ľavostranná ( <80 kg ) ; pravostranná ( >120kg ) ; dvojstranná ( sa nerovná 100 kg )

Ako to funguje?

Celý test je o jednej jedinej záležitosti: potvrdiť/nepotvrdiť nulovú hypotézu na stanovenom intervale spoľahlivosti.

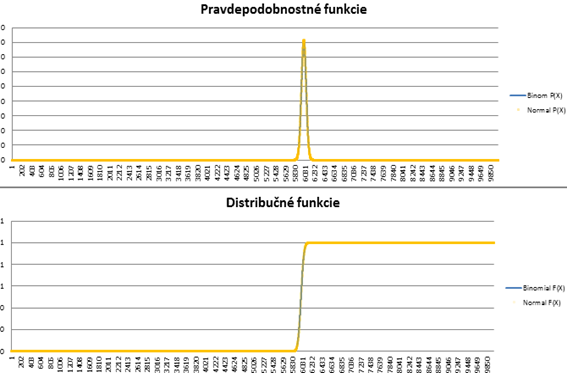
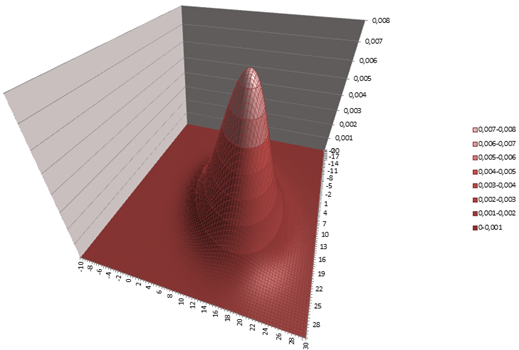
Ak si spomeniete na Normálne rozdelenie – viď článok, pamätáte sa na fakt že:

Normálne rozdelenie a obecne ak sa jedná o pravdepodobnostné rozdelenie – nemá uzavretý definičný obor. ( Koľkokrát padne na kocke číslo 6? My sme si empiricky overili, že to je 4-krát ale tá 6-tka nám môže padnúť aj 12x za sebou..aj 30x až….teoreticky to je možné aj keď prakticky s tým málokto počíta! ).

Práve to je dôvod, keď tvrdenie nemôžeme s istotou deklarovať ( vyprodukujeme 100 kg ), no môžeme ho podporiť istou mierou spoľahlivosti!

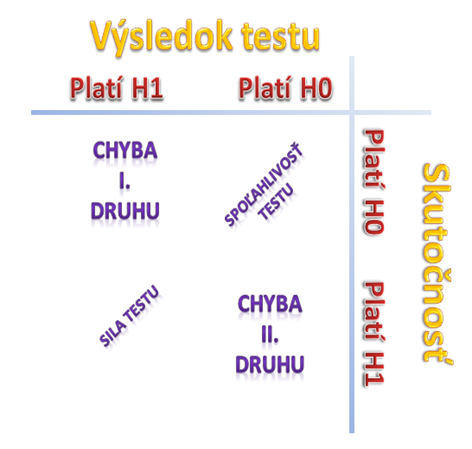
Tento obrázok porovnáva výsledok štatistického testu a skutočnosti. Pojem miera spoľahlivosti z predchádzajúcej vety je:

pravdepodobnosť, “istota alebo šanca” že náš test pravdivo potvrdí nulovú hypotézu, teda predpoklad.

Sila testu je niečo obdobné, akurát ňou ilustrujeme správne vyvrátenie nulovej hypotézy – potvrdenie alternatívnej

Ostatné možnosti sú chyby našej analýzy hypotéz. V praxi sa snažíme dospieť k vyváženému pomeru sily testu a miere spoľahlivosti. Obecne sa určuje miera spoľahlivosti 0,95 alebo 0,99.

Všeobecne sa označuje:

1) miera spoľahlivosti: 1-α

2) Sila testu 1-β

3) Chyba I. druhu: α (taktiež nazývame hladina významnosti)

4) Chyba II. druhu: β

Nabudúce si ukážeme niektoré vzorové príklady testovania hypotéz a možno použijem aj iný software ako Excel. Takže máte sa načo tešiť!

Chí-kvadrát rozdelenie

 

Som veľmi rád, že sa pomaly a isto dostávame k tematickému koncu a preto nebudem chodiť okolo horúcej kaše a začnem.

Pamätáte sa na pojem Normovanie? Ak nie skúste listovať v pamäti alebo v skôr narodených článkoch, pre nedočkavých stačí kliknúť na slovo Normovanie.

Spomeniem fakt, že normovaná veličina U_i je normálne rozdelená s parametrami:

Ľudské potreby sú však nevyspytateľné, obzvlášť v pitvaní sa v dátach čo viedlo k poznávaniu nasledujúcej štatistiky:

Využíva sa v rôznych oblastiach, ako príklad spomeniem testovanie závislosti kategoriálnych premenných v kontingenčnej tabuľke. Prejdime k hustote pravdepodobnosti:

 

V tomto prípade máme zadanú podmienku prirodzeného čísla pre chí-kvadrát štatistiku. V prípade nesplnenia podmienky je hustota rovná nule.

Momentová vytvárajúca funkcia spolu so základnými charakteristikami vyzerá nasledovne:

Tým pádom vám už nič nebráni k tomu, aby ste si stiahli sample file a pozreli si model rozdelenia a použité vzorčeky:

Ako ste si určite všimli, pre modelovanie som nepoužil žiadnu funkciu, ktorá by pripomínala pojem Chí kvadrát ale Gama rozdelenie! Ja som Vám totiž zatajoval celkom dôležitý fakt:

Chí kvadrát rozdelenie je konkrétny typ Gama rozdelenia, pre ktoré platí:

Vďaka tomuto poznatku som mohol namodelovať rozdelenie nasledovne:

Hustota pravdepodobnosti:

=GAMMADIST($D$2;$B$2;2;FALSE)    =GAMMADIST( X ; v/2 ; 2 ; FALSE )

Distribučná funkcia:

=GAMMADIST($D$2;$B$2;2;TRUE)      =GAMMADIST( X ; v/2 ; 2 ; TRUE )

Aby ste nepovedali, že som skúpy na informácie, prezradím vám ďalší vylepšovák: Ak je ν (tiež sa nazýva stupeň voľnosti) dostatočne veľké, povedzme že väčšie ako 30, môžeme aj toto rozdelenie definovať tzv. Fischerovou aproximáciou: 

Kde u_p je kvantil normovaného normálneho rozdelenia. Na záver článku a taktiež tematického celku by som chcel ako bonus pridať súbor, ktorý som vypracoval v rámci úlohy o Weibullovom rozdelení (mal príjemne pozitívnu odozvu). V ňom samozrejme nezabudnite povoliť makra a ak sa dostanete do VBA prostredia (Alt + F11), môžu vám základné makra poslúžiť ako inšpirácia.

Logaritmicko-normálne rozdelenie (modelovanie)

 

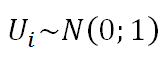
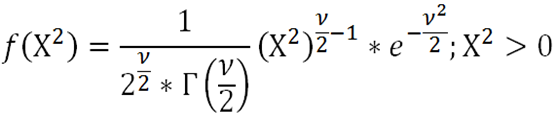
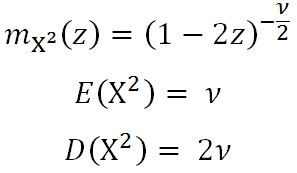
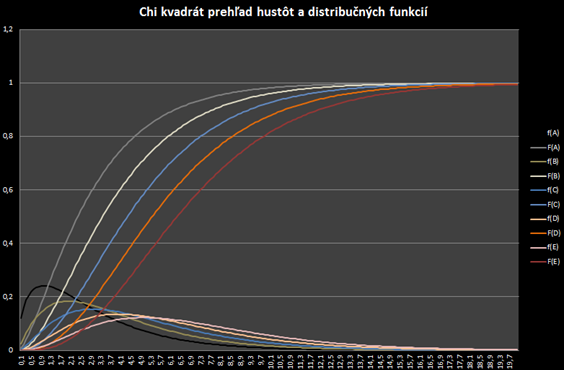
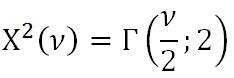
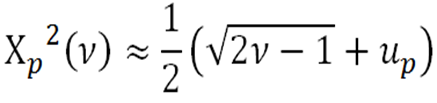
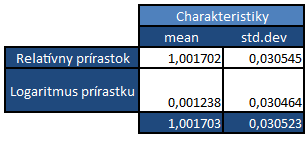
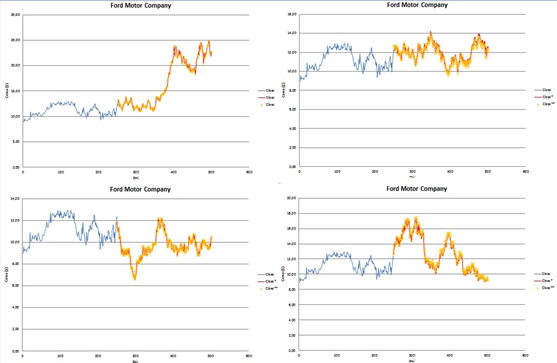
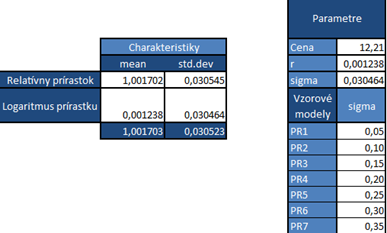
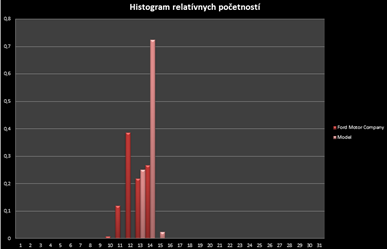
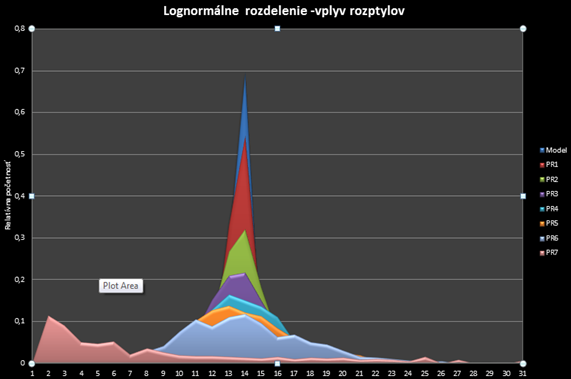
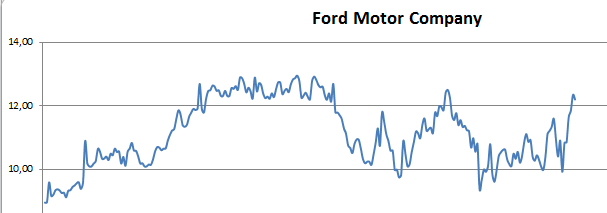
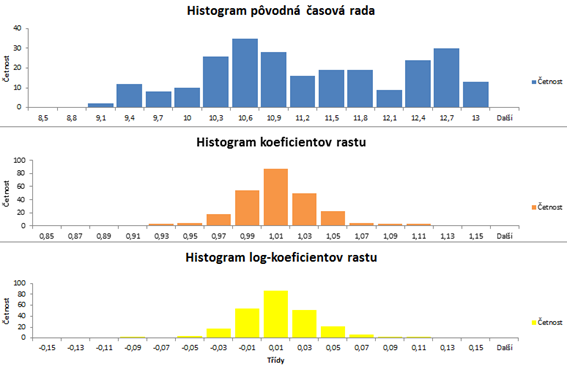
V predchádzajúcom článku sme si zobrali pod lupu akcie automobilky Ford Motor Company a ukázali, že ich zlogaritmované koeficienty rastu sú približne normálne rozdelené. Tento poznatok je kľúčový v štatistike aplikovanej vo financiách aj keď v praxi sa skoro každý stretne s problematikou tzv. fat tails a špicatejšieho pravdepodobnostného kopčeka.

My sa pre dnešok budeme zaoberať modelovaním log-normálneho rozdelenia na základe charakteristík, vývoja kurzu akcií Ford Motor Company (viď predchádzajúci článok).

Ponechajme si dáta zo sample file-u v minulom článku a pokúsme sa odhadnúť strednú hodnotu a rozptyl log-normálneho rozdelenia.

 

Pre strednú hodnotu sme použili, populárnu funkciu =average()  a smerodajné odchýlky zase =STDEV.S().

Hodnoty v modrom riadku sú vypočítané charakteristiky normálneho rozdelenia, pri znalosti µ a δ² z log-normálneho (skoro zhodné s  charakteristikami relatívneho prírastku).

V tomto prípade to znamená, že my môžeme budúce ceny modelovať normálnym alebo log-normálnym rozdelením!

Prečo potom log-normálne rozdelenie má svoje opodstatnenie???

Vo financiách sa každý stretol so spôsobmi úročenia. Jednoduché, zložené, zmiešané apod. no v konečnom dôsledku sa pri väčšine výpočtoch a oceňovaní derivátov používa spojité úročenie.

Čo sa týka limitného vzťahu, nebudem ho rozoberať (Google it! ), spomeniem však základný vzorec, z ktorého vyplýva opodstatnenie prirodzeného logaritmu v spojení s úrokom – koeficientom rastu pri cenách akcií.

 

Kde čas t je relatívne vyjadrené časové obdobie vzhľadom k určenej úrokovej (rastovej) miere r.  Ak je spojitá miera r vyjadrená na ročnej báze, bude potom jeden rok vyjadrený číslom 1, pol roka 0,5 atď.. A keďže každá úroková miera sa môže transformovať na spojitú, takto si pri rôznych úlohách zjednodušíme počty použitím spojitého úročenia.

Vráťme sa však k akciám a uvažujme dve dôležité vlastnosti:

1) Nulová autokorelácia

2) Stacionarita časovej rady

Potom môžeme na základe modelovania rastových koeficientov (ich logaritmov) určiť budúce ceny akcie takto:

Červená a žltá časová rada je predikcia vývoja cien akcie za stanovených podmienok, teda zjednodušený model, ktorý vyzerá nasledovne:

=$K$2*LOGNORM.INV(RAND();$K$3;$K$4)

 

=S_i*LOGNORM.INV(RAND();S_log-priemer;δ_log-výnosu)

alebo cez normálne rozdelenie:

=B252*NORM.INV(RAND();$M$4;$N$4)

 

=S_i*NORM.INV(RAND();S_priemer;δ_výnosu)

Takto nagenerujeme hodnoty ceny akcie pre S_i+1, ; S_i+2, ; S_i+3, …. atď. V porovnaní s realitou je to zjednodušená verzia, lebo všeobecne časové rady zápasia s mnoho problémami ako sú heteroskedasticita, autokorelácia, nestacionarita. Preto v praxi sa používajú trocha odlišné modely, ktoré sú napríklad sezónne očistené, dynamizujúce apod..

Teraz sa pokúsim priblížiť pohľad na vec prostredníctvom rozptylu, ktorý sa bude zväčšovať takto:

Máme k dispozícii poslednú cenu akcie, priemernú hodnotu zlogaritmovaného výnosu a taktiež log-smerodajnú odchýlku. Na základe týchto parametrov sme urobili model pre danú akciu a potom, následnou zmenou smerodajných odchyliek vytvorili ukážky modelov PR1 až PR7.

Ak sa vrátim k skutočnosti a modelu, je vidieť značný rozdiel v špicatosti modelu a zároveň, že model dostatočne nedemonštruje výskyt relatívne hrubých koncov rozdelenia. Čo sa týka ostatných vlastností rozdelenia, za zmienku stojí šikmosť, ktorá sa zmenou smerodajnej odchýlky mení.

Čím je menšia, tým rozdelenie sa blíži k symetrickému, no ak hodnota smerodajnej odchýlky prevýši hodnotu 1, rozdelenie sa zošikmí doľava.

Tento prípad zobrazuje nasledujúci obrázok, v ktorom model PR7 má v porovnaní so vstupnou tabuľkou pozmenenú smerodajnú odchýlku rovnú 2.

Tento typ grafu som uprednostnil pred klasickým stĺpcovým kvôli prehľadnosti jednotlivých modelov log-normálneho rozdelenia. Je evidentné, že s väčším rozptylom sa kopček spľaskne do viacerých cenových kategórií, tým pádom akcia má väčšiu tendenciu rapídne meniť cenu.

Nabudúce nás čaká ešte jedno, možno dve rozdelenia a potom dvere k iným zaujímavostiam, pre zmenu z fundamentálnej analýzy akcií.

Logaritmicko-normálne rozdelenie

 

Na úvod začneme burzou. Ukážeme si, v akom zmysle má Logaritmicko-normálne rozdelenie význam. No na začiatok by sme potrebovali dáta.

Navštívime stránku http://www.google.com/finance v ktorej si nájdeme titul ľubovoľnej akcie. Ja som si zvolil Ford Motor Company:

Klikneme na Historical prices a potom stiahneme historické ceny do súboru v Excel-i. Dáta sa uložili do formátu .csv tým pádom si ich musíme spracovať do použiteľnej podoby. Použijeme možnosť Text-To-Columns, ktorý som opísal v jednom z úvodných článkov. Ďalej môžeme vymazať všetky stĺpce okrem Close. Všimnime si dôležitý poznatok, t.j. hodnoty sú uložené ako dátum! Je to dosť nepríjemná záležitosť a my potrebujeme mať hodnoty vo formáte číslo s oddeľovačom desatinných miest čiarkou!

Ako na to?

1) stĺpec Close skopírujeme do Word súboru a nahradíme znak bodka - “ . “ čiarkou - “,”

2) potom dáta z Word-u skopírujeme späť do Excel-u a upravíme ich na formát číslo

 

Tento “prenos” do Word súboru odporúčam urobiť v zmysle zbavenia sa formátu ako dátumu. Takto prenesené dáta sú v podstate kľúčové hodnoty, v ktorých stačí urobiť náhradu bodky čiarkou (Ak by sme sa pokúsili nahradzovať v Excel-i, dostali by sme nežiaduci formát: dd,mm,rrrr). Výsledná časová rada by mala vyzerať nasledovne:

Takto ošetrené dáta sú pripravené na analýzu! Pomocou histogramu si môžeme analyzovať charakter časovej rady. Budeme sa snažiť priblížiť tvaru normálneho rozdelenia. V nasledujúcom obrázku budete mať náhľad histogramov pre pôvodnú časovú radu, potom pre  medzi-denný koeficient rastu a nakoniec logaritmická transformácia daného koeficientu(viď sample file).

Nakoľko sa svetlo-sfarbené histogramy podobajú, vhodnejšie je uvažovať transformáciu logaritmom z dôvodu nižšieho rozptylu ale hlavne:

Tým pádom môžeme konštatovať, že náhodná veličina ln(Y) má normálne rozdelenie. Otázka však znie, aké rozdelenie bude mať veličina Y ? Odpoveď znie Logaritmicko-normálne a spôsob, akým ho môžeme odvodiť je pomocou tzv. funkcie náhodných veličín!  Nakoľko sa jedná o celkom obsiahly proces, nebudem ho rozpitvávať, len uvediem dôležitý predpoklad:

Funkcia musí byť spojitého/hladkého charakteru pre celý definičný obor (existuje derivácia)!

Naša funkcia logaritmu je hladká v intervale nezáporných čísel (koeficient rastu je vždy kladné číslo). Vďaka tomu bude rozdelenie veličiny Y –> koeficient rastu (základná štatistika pri časových radách) vyzerať nasledovne:

Takto vytvorené rozdelenie má nasledujúce charakteristiky polohy a variability:

Pamätajte, hodnoty µ a δ² sú stredná hodnota a rozptyl pre veličinu ln(X), ktorá je normálne rozdelená. Avšak ak budeme uvažovať len veličinu Y, vyššie uvedené charakteristiky pre ňu platia ako log-normálne rozdelenú. Na budúce si namodelujeme log-normálne rozdelenie na základe stiahnutých dát.

Všetky cesty vedú do Ríma (k Normálnemu rozdeleniu)

 

V súčasnosti, dávam Normálnemu rozdeleniu veľký priestor v článkoch, no ako sami vidíte – je to potrebné. Existujú isté cesty, alebo povedzme dôkazy pomocou ktorých si môžeme zjednodušiť štatistický život tak, že budeme používať user friendly - Normálne rozdelenie. My si totižto empiricky ukážeme, že Binomicky, Poissonovo rozdelenú a všeobecne akúkoľvek náhodnú veličinu môžeme pri dostatočnom množstve dát bezpečne popísať Normálnym rozdelením vďaka ich aproximácii.

Jedná sa o tzv. limitné vety. No na začiatok si ukážeme, že Binomické rozdelenie pri veľkom počte možných náhodných javov a nízkej pravdepodobnosti aproximuje k Poissonovmu rozdeleniu.

V priloženom sample file-e si môžete prezrieť výpočty, no ako ilustrácia poslúži obrázok grafov rozdelení pre rôzne parametre binomického rozdelenia:




Moivreova-Laplaceova veta

Uvažujme proces, ktorým by sme mohli generovať možné výsledky náhodnej veličiny. Povedzme Alternatívnym rozdelením by sme generovali hodnoty x₁ ; x₂ … atď. Každá hodnota je generovaná nezávisle na výsledku predchádzajúcich hodnôt (Dôležitý predpoklad!).

Čo s takto danými hodnotami náhodných veličín? Môžeme uvažovať napríklad ich úhrn. V praxi si predstavíme zjednodušenú prípadovú štúdiu:

Každý sa na pár minút zahrá na poistného matematika v malej krajinke s 10 000 obyvateľmi. Keďže krajinka vznikla nedávno, všetci jej obyvatelia sú ekonomicky aktívni – odvádzajú peniaze na dôchodkové sporenie! Takto každý z nich musí odvádzať ešte 40 rokov istú čiastku, ktorú my ako ministri krajinky potrebujeme odhadnúť!

Zistime odhad množstva ľudí, ktorí o 40 rokov budú poberať dôchodok. Keďže naši spoluobčania musia tvrdo pracovať, aby našu maličkú ostrovnú krajinku postavili na nohy, povedzme že ich pravdepodobnosť dovŕšenia dôchodkového veku je 0.6.  To znamená, že štyria z desiatich sa dôchodku nedožijú a preto odvádzali peniaze nadarmo!

Dostaneme 10 000 náhodných veličín z Alternatívneho rozdelenia a nás zaujíma úhrn, t.j. množstvo budúcich dôchodcov o 40 rokov! Táto štatistika je už samozrejme Binomicky rozdelená a na základe Moivreovej-Laplaceovej vety pri veľkom počte ľudí môžeme tvrdiť, že: Ak sa ešte pamätáte na normovanie, potom nasledujúci kľúčový vzorec pre vás nebude problém pochopiť:

Výsledok zobrazuje nasledujúci obrázok:

Vzhľadom k takmer identickej podobe (použil som priehľadný typ dátovej čiary - vidieť tmavé sfarbenie binomického rozdelenia) môžeme hravo použiť pri výpočte očakávaného počtu dôchodcov Normálne rozdelenie. Problém výpočtu sumy, ktorú budú musieť spoluobčania platiť po dobu 40 rokov necháme pre ozajstných poistných matematikov a našu hru ukončíme . 

Lindeberg – Lévy

Táto tzv. zovšeobecnená verzia predchádzajúcej uvažuje akéhokoľvek rozdelenie  (identicky rozdelené a nezávislé náhodné veličiny). V tomto prípade musíme vedieť odvodiť konečnú strednú hodnotu a rozptyl.

 

Pamätajte na dôležitú vec! Pri manipulácii s normovaním je potrebné disponovať veľkým výberovým súborom (číslo n).

V prípade nesplnenia dostatočnej veľkosti hrozí, že váš prieskum nebude mať kvalitnú vypovedaciu schopnosť. Z hľadiska opodstatnenia veľkosti výberového súboru vám postačí nazrieť späť na prvý obrázok s ilustráciou Poissonovho a Binomického rozdelenia.

Budúci článok budeme rozoberať dôležitosť log–normálneho rozdelenia a taktiež prvýkrát použijeme dáta z reality (ceny burzovo obchodovaného titulu).

Normálne rozdelenie–3. diel

 

Dostávame sa do ďalšej fázy skúmania normálneho rozdelenia, v ktorej si namodelujeme dvojrozmerný typ – pravdepodobnostný kopček.

Uvažujme vektor náhodných veličín:

Modelovaním danej funkcie dostaneme pravdepodobnostný kopček. Vrátim sa však k charakteristikám, ktoré nebudem odvodzovať, len ich pomenujem. Sú to tzv. podmienené charakteristiky, ktoré sú celkom dôležité a používajú sa v regresnej analýze.

Podmienená stredná hodnota:

Ako ste si už všimli postrehnúť, táto podmienená stredná hodnota nie je konštantná, mení sa v závislosti od vstupnej vysvetľujúcej premennej. V praxi môžeme pomocou vysvetľujúcich (vopred známych) premenných modelovať vývoj vysvetľovanej premennej.

Táto funkcia sa odborne nazýva regresná. V tomto prípade uvažujeme priamku, ako typ, ktorým chceme popísať vysvetľovanú premennú.

Otázku regresnej analýzy budem podrobne rozoberať o niečo neskôr, až prejdeme nutné štatistické základy.

Podmienený rozptyl:

Podmienený rozptyl je vo svojej podstate konštantný (vstupné štatistiky poznáme z historických dát).

Táto vlastnosť sa taktiež nazýva homoskedasticita. V prípade regresnej analýzy je veľmi dôležitým predpokladom k tomu aby použitie regresnej analýzy bolo opodstatnené! V praxi pri analýze rôznorodých časových rad sa prakticky nepohnete bez toho, aby ste nezápasili s heteroskedasticitou.

Dané problematiky patria ku komplexným, preto je potrebné im venovať viac riadkov . Vráťme sa k modelovaniu nášho kopčeka. Aby ste nezúfali, ponúkam vám sample file na stiahnutie, stačí pozorne prejsť článok spolu so sample file-om.

1) Vypočítate zo vstupných dát potrebné charakteristiky, viď predchádzajúci článok

2) Pripravíte si dvojrozmerné rozhranie

3) Vyplníte “štvorec” pravdepodobnostnou funkciou, odkazujúcou sa na bočné/hraničné hodnoty takto:

=1/(2*PI()*$A$16*$B$16*SQRT(1-POWER($B$22;2)))*EXP(-1*(2*(1-POWER($B$22;2)))*(POWER(($I8-$A$18);2)/$D$15+POWER((K$1-$B$18);2)/$E$16-2*$B$22*($I8-$A$16)*(K$1-$B$18)/($A$18*$B$18)))

Pre ilustráciu som farebne oddelil hodnoty pred mocninou Eulerovho čísla. Dôležité je správne ukotviť bunky tak, aby sa pri kopírovaní posúvali vstupné hodnoty správne, pamätajte že:

$A$16 ukotvuje riadok aj stĺpec, takže sa vstupná hodnota pri kopírovaní nemení

$A16 ukotvuje stĺpec, takže pri kopírovaní vzorca sa vám budú hodnoty posúvať po ukotvenom stĺpci

A$16 ukotvuje riadok, takže pri kopírovaní vzorca sa budú meniť hodnoty podľa stĺpcov, teda budú sa posúvať po vopred stanovenom riadku.

4) Vyplnený dátový štvorec zobrazíme prostredníctvom 3D grafu, upravíme podľa chuti a máme hotový kopček.

V mojom sample file-e kopček vyzerá nasledovne:

V budúcom diele budeme pokračovať normálnym rozdelením. Mám pre vás potešujúcu správu, čakajú nás ešte aproximácie a normálne rozdelenie pre zlogaritmované hodnoty. Potom sa budeme zaoberať ešte dvomi-tromi rozdeleniami a prejdeme na zaujímavejšie články - budeme oceňovať akcie.

Normálne rozdelenie (Doplnok)

 

V dnešnom článku sa budem musieť vyjadriť k štatistikám, ktoré som použil pri modelovaní viacrozmerného normálneho rozdelenia. Jedná sa o kovariančný a korelačný koeficient. Tieto pojmy sú dôležité a to z hľadiska závislosti náhodných veličín medzi sebou.

Práve otázka popisu náhodných veličín rozhoduje o tom, či môžeme definovať silu lineárnej alebo celkovej závislosti medzi veličinami.

Ak sú dve náhodné veličiny normálne rozdelené, koreláciou nemeriame iba lineárnu závislosť!

Tento fakt sa dá dokázať odvodením marginálnych rozdelení z dvojrozmerného normálneho rozdelenia podľa ktorého platí:

Súčin marginálnych hustôt z dvojrozmerného normálneho rozdelenia je rovný združenej funkcii (nezávislosť náhodných veličín) len v prípade, ak korelačný koeficient (obecne považovaná lineárna nezávislosť) je rovný 0! Táto veta platí aj naopak.

Obecne ide o to, že v prípade normálne rozdelených veličín môžeme prostredníctvom korelačného koeficientu uvažovať závislosť obecnú a nie len lineárnu. Táto skutočnosť neplatí u iných pravdepodobnostných rozdelení.

Kovariančný koeficient

Táto štatistika sa obecne podobná rozptylu, no ak uvažujeme dve rôzne náhodné veličiny, vzorec bude vyzerať tak trocha inak:

Vo výpočtovom tvare:

Jeho úlohou je popísať silu lineárnej závislosti medzi veličinami. Obecne nadobúda kladných aj záporných hodnôt bez intervalovej obmedzenosti. Ak sa hodnota blíži 0, veličiny sú lineárne nezávislé. Pri kladných hodnotách sú veličiny priamo závislé (zväčší sa hodnota prvej, mala by sa zväčšiť hodnota druhej), pri záporných hodnotách platí opačný vzťah.

Nevýhoda koeficientu spočíva v jeho neohraničených hodnotách! Obecne je ťažké posúdiť, aký je rozdiel medzi kovarianciou 56 a 156. Môžeme sa maximálne domnievať, že tie veličiny sú priamo závislé.

Z tohto dôvodu sa v štatistike modifikoval na iný koeficient tak, že jeho hodnota je predelená násobkom smerodajných odchyliek náhodných veličín: 

Výpočtový tvar vyzerá takto:
 

 

Výhoda korelačného koeficientu spočíva v konečnosti hodnôt od -1 do 1. Hodnoty blížiace sa 0 indikujú lineárnu nezávislosť. Inak platia obdobné vzťahy ako pri kovariančnom koeficiente.

Prejdime na Excel, v ktorom vám v sample file-e ukážem, ako tieto štatistiky spočítať.

Kovariančný koeficient:

=COVARIANCE.S(Náh. veličina 1; Náh. veličina 2)

Použil som formulu s koncovkou „S“, ktorá vypočíta koeficient priamo zo vzorku, teda nie aproximuje hodnotu na populáciu.

Korelačný koeficient:

=CORREL(Náh. veličina 1; Náh. veličina 2)

 

 

Týmto stručným prehľadom som potreboval osvetliť  tieto dva dôležité štatistické pojmy. V budúcom článku pokračujeme v Normálnom rozdelení a budeme si modelovať „kopček“.